This is a follow up to classes I taught that included a short section on pricing research methodologies. I promised some more details on the Van Westendorp approach, in part because information available online may be confusing, or worse. This article is intended to be a practitioner’s guide for those conducting their own research.
First, a refresher. Van Westendorp’s Price Sensitivity Meter is one of a number of direct techniques to research pricing. Direct techniques assume that people have some understanding of what a product or service is worth, and therefore that it makes sense to ask explicitly about price. By contrast, indirect techniques, typically using conjoint or discrete choice analysis, combine the price with other attributes, ask questions about the total package, and then extract feelings about price from the results.
I prefer direct pricing techniques in most situations for several reasons:
- I believe people can usually give realistic answers about price.
- Indirect techniques are generally more expensive because of setup and analysis.
- It is harder to explain the results of conjoint or discrete choice to managers or other stakeholders.
- Direct techniques can be incorporated into qualitative studies in addition to their usual use in a survey.
Remember that all pricing research makes the assumption that people understand enough about the landscape to make valid comments. If someone doesn’t really have any idea about what they might be buying, the response won’t mean much regardless of whether the question is direct or the price is buried. Lack of knowledge presents challenges for radically new products. This aspect is one reason why pricing research should be treated as providing an input into pricing decisions, not a complete or absolute answer.
Other than Van Westendorp, the main direct pricing research methods are these:
- Direct open-ended questioning (“How much would you pay for this”). This is generally a bad way to ask, but you might get away with it at the end of a in-depth (qualitative) interview.
- Monadic (“Would you be willing to buy at $10”). This method has some merits, including being able to create a demand curve with a large enough sample and multiple price points. But there are some problems, chief being the difficulty of choosing price points, particularly when the prospective purchaser’s view of value is wildly different from the vendor’s. Running a pilot might help, but you run the risk of having to throw away results from the pilot. But if you include open-ended questions for comments, and people tell you the suggested price is ridiculous, at least you’ll know why nobody wants to buy at the price you set in the pilot. Monadic questioning is pretty simple, but it is generally easy to do better without much extra work.
- Laddering (“would you buy at $10”, then “would you buy at $8” or “would you still buy at $12”). Don’t even think about using this approach, as the results won’t tell you anything. The respondent will treat the series of questions as a negotiation rather than research. If you wanted to ask
about different configurations the problem is even worse. - Van Westendorp’s Price Sensitivity Meter uses open-ended questions combining price and quality. Since there is an inherent assumption that price is a reflection of value or quality, the technique is not useful for a true luxury good (that is, when sales volume increases at higher prices). Peter Van Westendorp introduced the Price Sensitivity Meter in 1976 and it has been widely used since then throughout the market research industry.
How to set up and analyze using Van Westendorp questions
The actual text typically varies with the product or service being tested, but usually the questions are worded like this:
- At what price would you think product is a bargain – a great buy for the money
- At what price would you begin to think product is getting expensive, but you still might consider it?
- At what price would you begin to think product is too expensive to consider?
- At what price would you begin to think product is so inexpensive that you would question the quality and not consider it?
There is debate over the order of questions, so you should probably just choose the order that feels right to you. We prefer the order shown above.
The questions can be asked in-person, by telephone, on paper or (most frequently these days) online survey. In the absence of a human administrator who can assure comprehension and valid results, online or paper surveys require well-written instructions. You may want to emphasize that the questions are different and highlight the differences. Some researchers use validation to force the respondent to create the expected relationships between the various values, but if done incorrectly this can backfire (see my earlier post). If you can’t validate in real-time (some survey tools won’t support the necessary programming), then you’ll need to clean the data (eliminate inconsistent responses) before analyzing. Whether you validate or not, remember that the questions use open-ended numeric responses. Don’t make the mistake of imposing your view of the world by offering ranges.
Excel formulae make it easy to do the checking, but to simplify things for an eyeball check, make sure the questions are ordered in your spreadsheet as you would expect prices to be ranked, that is Too Cheap, Bargain, Getting Expensive, Too Expensive.
Ensure that the values are numeric (you did set up your survey tool to store values rather than text didn’t you? – if not another Excel manipulation is needed), and then create your formula like this:
IF(AND(TooCheap<=Bargain,Bargain<=GettingExpensive, GettingExpensive<=TooExpensive), OK, FAIL)
You should end up with something like this extract:
|
ID |
Too Cheap |
Bargain |
GettingExpensive |
TooExpensive |
Valid |
|
1 |
40 |
100 |
500 |
500 |
OK |
|
2 |
1 |
99 |
100 |
500 |
OK |
|
3 |
10 |
2000 |
70000 |
100 |
FAIL |
|
4 |
0 |
30 |
100 |
150 |
OK |
|
5 |
0 |
500 |
1000 |
1000 |
OK |
Perhaps respondent 3 didn’t understand the wording of the questions, or perhaps (s)he didn’t want to give a useful response. Either way, the results can’t be used. If the survey had used real-time validation, the problem would have been avoided, but we might also have run the risk of annoying someone and causing them to terminate, potentially losing other useful data. That’s not always an easy decision when you have limited sample available.
Now you need to analyze the valid data. Van Westendorp results are displayed graphically for analysis, using plots of cumulative percentages. One way is using Excel’s Histogram tool to generate the values for the plots. You’ll need to set up the buckets,so it might be worth rank ordering the responses to get a good idea of the right buckets. Or you might already have an idea of price increments that make sense.
Create your own buckets, otherwise the Excel Histogram tool will make its own from the data, but they won’t be helpful.
Just to make the process even more complicated, you will need to plot inverse cumulative distributions (1 minus the number from the Histogram tool) for two of the questions. Bargain is inverted to become “Not a Bargain” and Getting Expensive becomes “Not Expensive”. Warning: if you search online you may find that plots vary, particularly in which questions are flipped. What I’m telling you here is my approach which seems to be the most common, and is also consistent with the Wikipedia article, but the final cross check is the vocalizing test, which we’ll get to shortly.
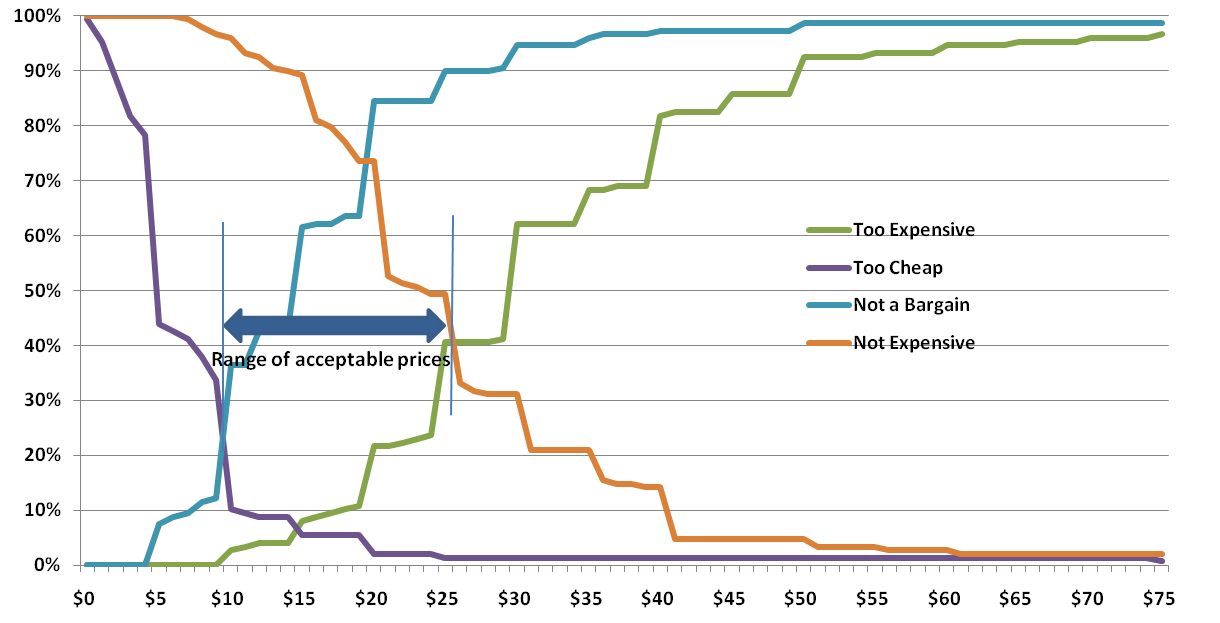
Before we get to interpretation, let’s apply the vocalization test. Read some of the results from the plots to see if everything makes sense intuitively.
“At $10, only 12% think the product is NOT a bargain, and at $26, 90% think it is NOT a bargain.”
“44% think it is too cheap at $5, but at $19 only 5% think it is too cheap.”
“At $30, 62% think it is too expensive, while 31% think it is NOT expensive – meaning 69% think it is getting expensve” (Remember these are cumulative – the 69% includes the 62%). Maybe this last one isn’t a good example of the vocalization check as you have to revert back to the non flipped version. But it is still a good check; more people will perceive something as getting expensive than too expensive.
Interpretation
Much has been written on interpreting the different intersections and the relationships between intersections of Van Westendorp plots. Personally, I think the most useful result is the Range of Acceptable Prices. The lower bound is the intersection of Too Cheap and Expensive (sometimes called the point of marginal cheapness). The upper bound is the intersection of Too Expensive and Not Expensive (the point of marginal expensiveness). In the chart above, this range is from $10 to $25. As you can see, there is a very significant perception shift below $10. The size of the shift is partly accounted for by the fact that $10 is an even value. People believe that $9.99 is very different from $10; even though this chart used whole dollar numbers, this effect is still apparent. Although the upper intersection is at $25, the Too Expensive and Not Expensive lines don’t diverge much until $30. In this case, anywhere between $25 and $30 for the upper bound would probably make little difference – at least before testing demand.
Some people think the so-called optimal price (the intersection of Too Expensive and Too Cheap) is useful, but I think there is a danger of trying to create static perfection in a dynamic world, especially since pricing research is generally only one input to a pricing decision. For more on the overall discipline of pricing, Thomas Nagle’s book is a great source.
Going beyond Van Westendorp’s original questions
As originally proposed, the Van Westendorp questions provide no information about willingness to purchase, and thus nothing about expected revenue or margin.
To provide more insight into demand and profit, we can add one or two more questions.
The simple approach is to add a single question along the following lines:
At a price between the price you identified as ‘a bargain’ and the price you said was ‘getting expensive’, how likely would you be to purchase?
With a single question, we’d generally use a Likert scale response (Very unlikely, Unlikely, Unsure, Likely, Very Likely) and apply a model to generate an expected purchase likelihood at each point. The model will probably vary by product and situation, but let’s say 70% of Very Likely + 50% of Likely as a starting point. It is generally better to be conservative and assume that fewer will actually buy than tell you they will, but there is no harm in using what-ifs to plan in case of a runaway success, especially if there is a manufacturing impact.
A more comprehensive approach is to ask separate questions for the ‘bargain’ and ‘getting expensive’ prices, in this case using percentage responses. The resulting data can be turned into demand/revenue curves, again based on modeled assumptions or what-ifs for the specific situation.
Conclusion
Van Westendorp pricing questions offer a simple, yet powerful way to incorporate price perceptions into pricing decisions. In addition to their use in large scale surveys described here, I’ve used these questions for in-depth interviews and focus groups (individual responses followed by group discussion).
Idiosyncratically,
Mike Pritchard
References:
Wikipedia article: http://en.wikipedia.org/wiki/Van_Westendorp’s_Price_Sensitivity_Meter
The Strategy and Tactics of Pricing, Thomas Nagle, John Hogan, Joseph Zale, is the standard pricing reference. The fifth edition contains a new chapter on price implementation and several updated examples on pricing challenges in today’s markets.
Or you can buy an older edition to save money. Search for Thomas Nagle pricing
Pricing with Confidence, Reed Holden.
The Price Advantage, Walter Baker, Michael Marn, Craig Zawada.
Van-Westendorp PH,(1976), NSS Price Sensitivity Meter – a new approach to the study of consumer perception of price. Proceedings of the 29th Congress, Venice ESOMAR
Hello,
I’m curious what are the risks of keeping in the illogical data? I’m working on a VW for a client and some are worried that it would reduce our n size too much to remove the respondents who fall out during validation (reduces n to 150 from 400). The results are quite different between the data with all respondents and that with just those who passed the validation step.
I’m also curious how you approach findings where the Optimal Price point is nearly identical to the point of marginal cheapness?
Thank you!
Thank you for your comment.
I’d say that keeping the “illogical” data (ie failing validation for any of the relationships between the pricing questions) is illogical (to re-use your Star Trek word). There are several possible reasons for you to have 62.5% of data that’s at least questionable, and may have worse consequences.
Real-time validation for the pricing section is a powerful enhancement that offers a number of advantages. I’m only going to touch on the concepts here because our approach is a trade secret and differentiator.
Before I move on to the second question you posed, you mentioned that “results are quite different between data from all respondents and validated responses”.
What about the spread? Have you compared variances etc.?
Finally, you asked what about when the “Optimal Price point is nearly identical to the point of marginal cheapness?”
We don’t obsess about the crossover points, although they are important to the inner workings of the PSM, particularly to create the range of acceptable prices, which is the most important output. But it’s a range, and setting the price isn’t just a matter of picking the Optimal Price Point. You haven’t provided much information about the category or the product/service to be able to go into much depth. I’m assuming from the 400 sample size, that this is a consumer product or service. but I can’t say much more. There is a lot of mumbo jumbo written about one intersection being to the left or right of another, or intersecting at higher or lower percentages, but I haven’t seen any with good rationale.
The Price Sensitivity Meter, combined with Demand analysis, provides good starting points for setting the price.
I hope this has been some help. A private conversation would be the logical next step.
Mike
Hello, The labels in your table and in your chart do not match.
In the table you have “Bargain” and “Getting Expensive”,
But in your chart you have “Not a Bargain” and “Not Expensive”
Does table “Bargain” = Chart “Not Expensive” and table “Getting Expensive” = chart “Not a Bargain”?
Thanks.
Jennie, I’m sorry for the confusion. The table includes the questions as asked, corresponding to the questions shown in an earlier paragraph. The calculations that generate the lines in the chart include generating cumulative percentages for all four questions, and reversing the sense for two of the questions. So Bargain becomes Not a Bargain, and Getting Expensive becomes Not Expensive.
We can look at what happens in a couple of other ways which might help explain:
This is what Van Westendorp intended, and it makes interpretation easier.
Does this help?
Hi Mike,
In a study that we are doing currently, we have asked the respondents for the interest to purchase at three price points – price expected to pay, price they consider a good bargain and the price which starts getting expensive for them.
In this scenario, with three questions asking for their likelihood to purchase, how would you suggest we create the demand curve?
Thanks,
Sanskriti
Hi Sanskriti, thanks for asking the question. You didn’t explain what product or service is being covered, and I’m wondering why you didn’t include the question about too inexpensive. That’s really critical in my opinion. Re-reading your comment, perhaps I’m misunderstanding your technique and you included the question for prices, but not for demand. But I’m not sure what you were intending to get at with the “price expected to pay” question. That seems like a way to confuse people by asking in two different manners. It’s as if you are asking for their input and then saying “you might not get the price you would like, and what would you expect to have to pay”. I’d be interested in your response on this.
However, to your specific question, let me suggest that you use the questions for bargain and getting expensive as the basis for a follow-up question on demand, as follows: “At a price between [bargain] and [getting expensive], how likely are you to buy?” The [bargain] and [getting expensive] values would ideally be actual numbers from the values they gave for the earlier questions; that’s the way we do it. You could change the wording a little if you are unable to get the survey programmed in that fashion. And you should include a time horizon – such as within the next three months, within six months of the product bring introduced, or the next time you are in the market for something like this. The question should be a Likert style question with very likely, somewhat likely, neutral, not very likely and not at all likely options.
I’m going to give you the synopsis of how we do the analysis for demand, and yet again I’m going to make a promise to get the real article written as soon as possible.
Choose percentages for the options to account for people giving over of over-optimistic responses to purchase likelihood questions. We use 70% for very likely (meaning that 70% of those who say they are very likely to purchase will actually buy), and 50% for somewhat likely, with 0% for the other options.
Use the same approach as for the basic van Westendorp graphical analysis by plotting cumulative percentages.
We use two Y axes with one showing the modeled demand (equivalent to market share), by multiplying the raw numbers of respondents who gave an answer between bargain and getting expensive and multiplying by the model for their purchase likelihood (0.7, 0.5, zero, zero, zero) divided by the total number of respondents.
The final step for the second demand chart using the second Y axis for revenue index by generating the potential revenue at each one of the price points and then dividing by the maximum revenue to provide a revenue index. The revenue index is more useful than an actual number because it doesn’t create confusion based on the sample size or not knowing the cost of the product or service.
By placing the demand and revenue lines on the same chart it is easy to see whether higher revenues can be achieved at higher prices. This isn’t as obvious as it might appear because each respondent is only included (at the appropriate modeled rate) for values that lie between their own bargain and getting expensive price points.
I suppose you could create the two charts separately for the bargain and getting expensive questions, and even – if you must – for expected price question. But I think that would be too many questions, too many charts and would create too much work to interpret in any meaningful way. After all, in the real world when faced with an opportunity to buy something you don’t necessarily have as many possibilities except perhaps for consumer commodities such as food. However, in favor of your approach, you would perhaps end up with more information about elasticity for individuals although elasticity for larger numbers of prospects is already in the charts we use.
Does this help?
Mike
Chris from HouseCanary pointed out a couple of places where the article could be improved. I hope the changes make it more readable. Thanks Chris!
Hi Mike,
I have a product that a client expects to price between USD 2000 and USD 3000. He does not want people to quote answers below USD 2000. Is it fine to specify a minimum value before administering the PSM ?
Rohan,
We often get asked similar questions to this. Here are a few thoughts for you to consider and share with the client as you see fit.
By asking questions this way, you can isolate the special cases from the rest without biasing everyone. You may learn additional valuable information, but in any case you aren’t undermining the basic Van Westendorp approach.
Does this make sense to you? I’d be interested to know whether your client is convinced by more explanation of the method, or if you use the follow up technique.
Mike
Looks like you might be still active in these comments five years on, so I’ll go ahead and ask. How many responses should we be looking for in this analysis? When I first heard about this, the presenter said that you only need about 10-20. Does this make sense?
Thanks for your comment David. When we run a survey with Van Westendorp pricing, we like to follow the rules of thumb – 400 minimum for consumer products/services, 200 minimum for business. The lower number for business is a matter of practicality as much as anything else. Sample costs a lot and is usually more difficult to acquire, so researchers live with greater ranges (±7% for 200, ±5% for 400 assuming a representative sample). However, we can’t always achieve the sample size goals. Still, the results from smaller samples are usually similar. The curves are less smooth, and the effects of price points are more pronounced. Another, potentially more serious, impact is that we don’t have as much ability to filter because we might only have a tiny sample in a group. We expect to see higher prices among those most interested; a smaller sample may limit the ability to discern these effects, or even worse deliver over-optimistic results.
We use Van Westendorp questions in interviews and focus groups, when the sample sizes are much lower – 10-20 responses are not uncommon. However, I would consider results from such a small sample size as directional, particularly when the interviewee and focus group participants are selected rather than a random sample. I’d say that 50 responses would be the minimum, 100 is better, and don’t expect too much from filtering.
Does this help?
Mike
mike,
Thanks for your article!
How can I create a demand curve from the “too cheap” and “too expensive” lines (I am guessing this demand curve will essentially encompass the area under the intersection of these two lines.)
Lino, thanks for your question. Creating a demand curve without asking a demand question will give you something that is overly theoretical or misleading. There are a couple of reasons for this.
This is foreshadowing the (long awaited) demand follow up. We ask a question about purchase likelihood at a price between the Bargain and Getting Expensive prices stated by the respondent earlier. (Some people use more than one question, but I prefer to keep it simple.) There is usually a time window – something like “within the next 3 months”. We use a 5 point scale (some use extended scales).
The results are modeled to determine which responses are included or not in the demand curve. Each price is checked for response to see if the price is within the Bargain to Getting Expensive window. Also, we discount some of the responses. Typically we count 70% of Very Likely, 50% of Somewhat Likely, and throw out everyone else because people will be more optimistic when answering a survey question than their true behavior. These values can be adjusted for what-if analysis. The result is a demand curve that usually peaks close to the point of lowest price resistance (the intersection of Too Cheap and Too Expensive). We go beyond the demand chart for revenue modeling, but that’s for another day.
Does this help?
Mike
Heller
I world like to know how I can make the inverse acumulative frequency ? for step by step or Where l Can find it
thank you
Thanks for your question Francisco. I’m hoping to find some more time soon to expand on some of the areas that keep coming up. However, I keep hoping without the time appearing, so let me just try to answer your question as directly as possible.
The process is something like this:
First, we perform validation and filtering on each response to generate a subset of the dataset for analysis. The validation is sometimes for each response (throw out the entire response if the relationships are not correct) or can be done between pairs of variables. The filtering is done to limit to the groups of interest. We may to include only people who are more interested, or who have other characteristics. The details aren’t important to your question; I just wanted to remind people that there is some preliminary work to generate the analysis dataset.
With the analysis dataset, we start working in columns. I’ll describe this part of the process as if it was all manual, but in practice most steps are automatic. We don’t use Excel’s cumulative distribution capabilities, instead the COUNTIF function is the key.
Using a column of price values to test, each pricing variable is tested against the price point to generate (in new columns) the number of responses below the current price point or above the price point. Use > and <=, or < and >= so that responses aren’t double counted.
The final step in generating the set of numbers that is used as the source for the chart is to turn the cumulative counts into percentages (of the total sample in the analysis dataset). It would probably be possible to combine this step with the step that generates the counts, but adding a few extra columns makes it easier to see what’s going on.
Does that help?
Yes,!
That help me very much!! Thank you for the help.
Other discurs, Why Van Westendorp puted acumulative frequency ? And Why the inverse ?
Are there other analysis ?
I am beging to make preview of price, quantity, and time using stocastic system.
I will use together with Van Westendorp
In your article you say, “The upper bound is the intersection of Too Expensive and Cheap (the point of marginal expensiveness). In the chart above, this range is from $50 to $100. As you can see, there is a very significant perception shift either side of the $50 and $100 price points.” However, the range of prices only goes up to $75. Am I missing something?
Ron, you definitely aren’t missing something. This section wasn’t updated after the chart was changed. Thanks for spotting the inconsistency. I’ve updated the text, with some additional points, hopefully helpful.
Thanks for the great article. I have done this many times in the past but the data set is weighted. Should I use the weighted data for this technique or revert to unweighted? Not sure how the weight might impact the results or if there is some agreed upon process for this. Thanks!
I’m glad you liked the article Holly. Weighting – that’s an interesting question. We normally run the charts on unweighted data, but typically using 2 or 3 filters for groups of interest. That isn’t the same as weighting, I know, but I usually find that splitting up this way shows distinctions that make sense – e.g. people who are more engaged in the area served by a new product are willing to pay higher prices. I suspect that this filtering might have more impact on results than weighting for, say, age or gender. However, logically, weighting would make sense. For instance, if males are inclined to pay more, yet the results contain more females, the results will be somewhat skewed.
Anyway, I’ve figured out a way to incorporate weighting. This is conceptual, but I’ve tested it with some data and a weighting variable based on randomization. Previously, I used the Excel COUNTIFS function to count the number of cumulative responses for each price point. To use weighting, use SUMIFS instead. Something like this (using Excel tables):
SUMIFS([WeightingVariable],[Bargain],">="&PricePoint)
If your weighting process doesn’t end up with the same total number of responses as you started with, you’ll need adjust the divisor for the percentages.
When I tested, I saw that the charts were a little different from the unweighted version, but not much. Of course, the difference is based on on my artificial weighting. I didn’t want to hold up a response while I searched for a dataset from a pricing study with relevant weighting.
Does this make sense?
Mike
Hi Mike – This article is very helpful! We’ve just conducted a study using Van Westendorp questions, without using programing logic to validate the responses in the field. Now as we look through the data, we’re wondering whether the number of invalid respondents we’re seeing is normal or not. Can you give us a sense of how many respondents typically give inconsistent answers to the Van Westendorp questions?
Thanks!
Hey Mike,
Thanks very much for your help! Looked like I didnt reverse the two lines – the charts make sense now, which has immensly helped with my study! Also liked your suggestions on purchase likelihood and wallet share. Much appreciated!
Hey Mike,
I’ve been using this model pricing and have plotted the data. Strangely, in one of my graphs the “too inexpensive” and “expensive” lines dont intersect and the “bargain” and “expensive” dont either. Is it okay to use trendlines to estimate the PMC & PME? Or do you think I’ve gone drastically wrong somewhere? Do advise. Thanks!
Hi Zaf,
It sounds like you may have done something wrong. Are you plotting the reverse cumulative percentages for the correct lines? That is – for “Too Inexpensive” and “Getting Expensive”? I don’t see how you could use trends to get the crossovers, but you could do it directly in Excel.
I’d be glad to take a look at the data for you if you like. I’m working on some improvements to the method I use to generate charts, so it would be fun to see how easy it is to deal with raw data.
If you do it yourself, please let me know how it turns out.
–Mike
Hi Taylor, thanks for your question. Did you get my email asking if you could send the data so I could take a look? I was hoping to give you an answer that others could benefit from.
–Mike
When I calculate my cummulative percentages, it only goes to 92%, not 100%. Any thoughts on what I’m doing wrong?
Hi Mike,
I just have a simple question – do you state the type of question inside the question?
For example,
What do you think is the highest price for a Honda Civic 2010 which will make you to never consider buying it? (too expensive)
Thank you
Hi Orde,
We don’t state the question type along with the question, but try to make the text clear enough so that additional explanation is not necessary. I’d rather frame the question in terms that relate to the respondent and the situation. For your example, I’d suggest a little editing.
What do you think is the highest price for a Honda Civic 2010 which will make you to never consider buying it?
To me, this is a little confusing and seems like a double negative. As a result, it isn’t as connected to the “too expensive” question as it should be. How about this instead?
At what price would a Honda Civic 2010 be too expensive so that you would not consider buying it?
We do emphasize the different words that distinguish between questions.
I hope this helps.
Mike
Hi Mike
I want to further explore the price volume relationship after the optimal price is generated. how is this best done? By asking questions like how likely are you to buy at (optimal price and plus/minus 10% from optimal price) and then following up with a question like “out of your next 100 purchases how many would you make at the optimal price and plus/minus 10%?
thanks
Dominic,
I’m sorry that I haven’t yet written the follow up that should make this exploration clearer. The approach we take is to ask a question like this:
At a price between X and Y, how likely are you to buy this product in the next six months?
X and Y are piped from the respondent’s answers to the Bargain and Getting expensive questions (some researchers might use Too Cheap and Too Expensive but I prefer to be more conservative). The future horizon text is product and situation specific (you might say after the product is introduced for something that isn’t in the market. We analyze by using a likelihood model (for example, 80% of the Very Likely, 60% of Somewhat Likely, ignore the others) and then calculating the percentage that would buy for each price. The result is an index of volume at various prices, and we usually also add an index for revenue too. If the volume doesn’t fall off too rapidly, the revenue index will show that a higher price is likely to be better – as long as it’s in the acceptable price window. [As I write this I can see that an article with some graphs will make it clearer].
Your suggested additions might work fine, but we are generally trying to keep to a reasonable time without having too many pricing questions. If you have a larger sample, you might be able to present a random price within the respondent’s window, or perhaps within the broader window of Too Cheap to Too Expensive. But I’ve seen surveys where the follow up question or questions use a price that is unacceptable. A survey taker thinks you are pretty dumb if she told you that the highest price she’d pay is $50 and then you ask “how likely would you be to buy if the price is $100?” Don’t do it.
Does this help?
A side question for you and anyone else reading: Would you be interested in a service that takes your data and turns it into charts so that you have the range of acceptable prices, and can incorporate into your reporting?
Mike
Hello Mike-
Thanks for the helpful post! I’m tracing your process with my own set of data, and I’m not clear on how the final histogram was built. Did you create one histogram from your four buckets of values, or four separate histograms? If they were separate, when you built one master chart, how did you set the x-axis to include all the data points and how they differ per bucket? Thanks!
Andrew, I’m glad you liked the post.
I’m actually not creating separate histograms any more, but my tool essentially uses four histograms – they just aren’t visible separately the way we do it. If you prefer to see the histograms you can use the Excel tools to generate histograms based on the data, or specify the buckets. After evaluating the ranges, you’ll find that you can use one set of x-axis values for all four charts. I usually truncate the range (most often at the high end, occasionally at the low end) to eliminate outliers when the rate of change is small.
I can see that I’ll have to revise the main article, not just write the second one!!
Mike
Hi Mike,
Thanks for this post. I’ve been learning how to do these analyses and your site was the most helpful from my extensive searching online.
I had two follow-up questions:
First, I’m not confident that I’m plotting my histogram properly. My prices range from 1-100, and so when I create my bins in the Histogram, I use 0-99 as my manual ‘bins’. Then, when I plot the data I use $1 for the ‘0’ bin and $11 for the ’10’ bin, and so forth. This is critical for me because obviously people will give numbers that break on regular intervals ($10, $20, etc.). In your interpretation above you wrote, “At $50, about 55% think it is a bargain.” Yet, depending on this binning issues and where the stairstep function occurs, I would have read your chart as “At $50, about 67% think it is a bargain”. Does that make sense?
My other question is the follow-up interpretation. I ask a single follow-up using the average of their “Bargain” and “GettingExpensive” prices about likelihood to purchase. To apply the model you casually referenced, do we just multiply the weightings by the respondent percentages? So, (60% multiplied by the “Probably buy” percentage), summed with (25% multiplied by the “Definitely buy” percentage)? I know there are many models, but is that what you meant by your one example? Do we factor at all the actual average price they used, before considering their answer to the likelihood issue? Does that get weighted in at all?
Thanks!
Mat, I’m glad you found the post helpful.
I need to go back and recheck the vocalizations. I believe the statements were intended to be general, or may have related to a previous chart, but I can see that it would make more sense to have them connect to the specific chart. I won’t attempt that tonight (I don’t usually do Van Westendorp analysis with a glass of wine in hand!). But yes, your comment makes sense. Of course, if you wanted to be more accurate/pedantic you could say that at just 68% state a price of just under $50 to be a bargain, while 55% think it is a bargain at just over $50.
Your second question is more complicated. I’m just getting ready to write a follow up (after the website revision) and I’m getting close to offering a service for the original VW plus the follow up. I usually ask the question in terms of “at a price between [Bargain] and [Getting Expensive]“, but your approach is similar, and has the advantage of offering a specific price that might be less burdensome. Yes, I use a model like yours for actual likelihood, with the percentages varying by the situation (and sometimes with client perceptions). The predicted demand is based on the likelihood model and the price falling within the limits for each person. So if someone’s Bargain price is $25 and their GettingExpensive is $60, their likelihood isn’t counted in demand at a price of $65. I think there are tradeoffs in how many questions to ask for follow up, and at what points. I’ll be exploring those issues in the next post on the subject.
Mike
Mike,
Thanks for the article — very helpful and informative. I do have one question: If price ranges were used in the questions instead of leaving them open ended, how would you handle that from an interpretive standpoint?
Thanks in advance for the response.
Zack Apkarian
Director, Retail Insights
Pfizer Consumer Healthcare
Zack, thanks for the kind words, and sorry for the delayed response.
I’ve been reviewing the literature (in between project work and overseeing a website overhaul). But I haven’t been able to come up with a reasonable way to use price ranges instead of open-ends. In fact, letting prospective purchasers choose their own price points is one of the main points in Van Westendorp’s Price Sensitivity Meter. From my experience with many studies, people really do give valid and useful information. Of course, they need to know enough about the product or service. I’ve certainly seen situations where the client didn’t like the results, and in one case they would probably have preferred a different style of question with fixed points, because the new product had already been pre-sold to management at a higher price. But the survey results proved more predictive – the product was released at too high a price and taken off the market within six months.
Back to your question. There are always some outliers that need to be eliminated. Some think that a price of zero is not too cheap, some are unrealistic and very high prices are stated. These get flushed out in the graphical analysis. But if you are absolutely convinced that your product should be within a certain range, and that despite giving all the information you can, people may still give the wrong answer without help, you could load the deck. That is, you could say something like “we are planning on a price of between X and Y“. Maybe something about “we are planning to introduce a product, exact features to be decided, at a price between X and Y“. This still doesn’t make a lot of sense to me.
The other thing you could do, is specify fixed prices in the follow up purchase likelihood question, instead of using their inputs. I’ve done this when I worked with another consultant who couldn’t convince the client to use Van Westendorp alone. The result was rather odd. Someone who stated that $80 was too high for them to consider would be asked how likely they would be to buy at $100.
But maybe this isn’t along the lines of your question. In any case, I’d love to talk more about it. Feel free to give me a call.
Mike
Mike: Interesting and useful article, as this is my first experience with VW. Are you aware of any software or Excel template that “automates” the data reduction?
Hi Joe. Sorry about the delayed response. I’m just about to release something that should do what you want, so watch this space….
Mike
Hi Mike,
I just ran the van Westendorp survey over a group of respondents and plotted the cumulative frequencies on a graph. The problem is my “Too Cheap” and “Too Expensive” lines don’t seem to intersect, so I couldn’t get the Optimal Price Point (OPP). They’re really close to intersecting, though. I have the rest of the intersection points IPP, PME and PMC. I tried running the survey over a bigger number of respondents, but there’s still no progress over this matter. What should I do? Should I just extend the lines and guess on an OPP? Something doesn’t feel right doing that though.. or should I just leave it the way it is? But how do I interpret my results then?
Sorry to bother you with all these questions. I’m really stuck on this matter, I hope you can offer me some help. Thanks for your time!
Hi Daniel. I’ve just been checking old comments. I was waiting for a private reply from you so I could do a more complete response, but maybe it went into your spam. I’d like to look at the data to better understand what’s going on.
But in general, your example is a good one to support my point that the most useful result from Van Westendorp analysis is the range of acceptable prices. Without knowing more about your study, I hesitate to speculate too much on the reasons, but here’s one scenario that might generate the results you describe. Imagine that the questions were being asked about a car. A car in general, not a specific car. The upper boundary for ‘Too Cheap’ could easily be quite low because people might be imagine a whole range of cars that would be available, perhaps including used cars. The lower point for ‘Too Expensive’ could be higher if people aren’t thinking about the same car for the two questions.
Does that help? If you want to send me some more information (ideally the data) privately I’ll be glad to take a look.
Mike
Hi Mike,
I was wondering if you could expand a bit on how to analyze/model the “going beyond” questions — if you use the two additional questions on likelihood to purchase — the bargain and getting expensive price points? Do you just use the price point they are most likely to purchase at (it would be the bargain price almost all the time wouldn’t it) or do you average the 2 price points when plotting the demand/revenue curves? Thanks for any guidance you can provide!
Hi Mark. Thanks for your interest. There are a couple of different ways to come up with demand/revenue curves. I’ll do an update or a new post shortly.
Mike
I found the problem and it is me. I got wildly different results because I screwed up two of the cumulative distributions in a way that is too complex to explain and would embarrass me even more than I already am. At least the problem is solved and whatever faith in the model we have has been restored.
Don’t be too hard on yourself Mark. Although the concept behind Van Westendorp is simple, it seems that it is also easy to make mistakes with the plots.
I’m glad you got it figured out.
Mike
I ran the model two ways. The first way, I broke the prices into increments of $1.50. The second way, I broke the prices into increments of $.25. I got wildly different results, based on how I grouped the prices. I checked and double-checked that I did everything correctly. Have you ever seen this before? It just doesn’t make sense that this would happen.
n = 306 consumers
Hi Mark, interesting results. Can you give more details on the ranges of values you got? How did the results vary?
I can imagine that there would be some differences if the product/service should be priced close to the increments. In other words, if the fair price is $2.50 say, you might have spiky results. That would be similar to any situation where there is a threshold and there are big jumps in that area. If there isn’t anything like that, I’m not sure what could be the cause.
Mike
Mike, couple of follow up questions:
1. Why is cumulative frequency used in this method?
2. What if vocalisation reveals that the results don’t make sense intuitively – do we reject the research outcomes? What flaw does it point to?
Anna, thanks for your interest.
Van Westendorp is a price optimization technique. The point where the Too Expensive and Too Cheap curves cross is called the point of marginal cheapness. This is where the fewest people will not buy because they consider the product too expensive or too cheap. So the maximum volume of product will be sold at this point. I usually place less emphasis on this point because it looks as if it gives a more precise result than the data generally supports – especially for products that are not all that mature or well-defined. However, it serves to illustrate the reason why the cumulative plots are valuable. To look at it another way, using the vocalization examples, at $300 only 5% think it is too cheap. But at $35, 40% think it is too cheap. The 40% who think $35 is too cheap includes the 5% who thought $300 too cheap.
The vocalization doesn’t cast doubt on the research results, it merely makes sure that you have plotted the curves correctly, and that you are comfortable talking about them in front of management and clients. If the results don’t make sense intuitively, that probably means that the respondents don’t understand the product well enough. Perhaps it is too new for them to appreciate the value proposition, or perhaps the information provided in the survey wasn’t adequate.
I hope this helps.
Mike
Very helpful writeup – thanks Mike!
I’m glad you found the article helpful Vetri. Let me know if there are other survey or research topics you’d like covered.